The Great Vacation: Recessions In DSGE Models (Part II)

The Great Vacation Effect is what I term one well-known pathological side effect of almost all macro dynamic stochastic general equilibrium (DSGE) models: since employment hours are a voluntary decision in the household optimisation problem the direct implication that unemployment is voluntary as well. As such, The Great Depression can be interpreted as The Great Vacation. Although this silliness is well known, the silliness has nasty side effects for recession analysis. This article continues the discussion of the previous part, turning to the question of why this effect matters even if we suspend disbelief with respect to the interpretation of unemployment. 

Background

My assumption in this article is that the reader is somewhat familiar with the structure of macro DSGE models. Key points were discussed in the first part, but I am not assuming that readers would have gone through it. Nevertheless, I will review the part of the model structure that I am interested in.

It is difficult to generalise about DSGE models, since this is an extremely wide class of models, and researchers are continuously adding new variations. There are classes of DSGE models that I do not classify as being macro models; at the minimum, they need to include two optimisation problems that have been fused together by a general equilibrium assumption. The first problem is the Household Optimisation Problem, the second is one for firms. This article only looks at the household problem, which is luckily broadly similar across DSGE macro models.

As discussed in Part I, the mathematical assumption is that households can take prices as given, and find an optimal path to maximise utility. When I write prices that refers to at least three prices: wages, goods prices, and interest rates (bond prices). Note that these variables are not just the spot levels, they include forward values (which are not directly measured in the case of wages). Since we are taking these prices as given, we can examine the behaviour of the household optimisation as a stand-alone problem. (As noted in Part I, I have to make the heroic assumptions that a solution to the DSGE model exists, is unique, and this model solution corresponds to the optimal solution of the household problem. If these assumptions are not true, the model is nonsensical, and we can learn nothing from it.)

Utility Maximisation

Let us now look at the utility maximisation problem. Although the details can vary, the following statements capture the behaviour of the variables that appear in almost all cases.

• Prices (wages, goods prices, interest rates) are taken as given, or exogenous to this problem.
• The level of utility is the discounted sum of single period utility values, with those values generally being a function of the consumption and hours worked in that period. (Some models might sneak in a money balances term, which I will ignore.) Future values are discounted back to a current value, since the sum of non-discounted utility terms on an infinite horizon would be infinite. (The discounting horizon is equal to the lifetime of the household agent, which is either a few periods of an overlapping generations model, or out to infinity for the representative household version.)
• There is a diminishing returns to consumption for adding to utility. Typically, consumption will taken to a power of less than 1. As an extremely simplified explanation as to why this is the case, imagine that a household can consume two units of goods over two time periods, with no discounting. If utility is given by the square root of consumption in each period the optimal choice is to consume 1 each period, giving a total utility of two. If the household decided to front-load consumption, they might consume 2 units first, then zero. The utility would be the square root of 2 (about 1.41), which is sub-optimal. Conversely, if utility was the square of consumption, the optimal strategy is to front load, since the utility is 4, versus 2 for an even distribution.
• In order to get a labour market that meets assumptions about supply and demand, there is negative utility associated with working. This prevents the household from working infinite hours to fund infinite consumption: at some point, the disutility of working overpowers the utility gains from consumption.
• The amount of consumption allowed is determined by a budget constraint. The household has to pay for all consumed goods from wages, or by selling financial assets, and possibly borrowing against future cash flows. (The identity of the lender is often not pursued, although there are variants where one representative household lends to another.)
• The effect of interest rates and financial asset holdings shows up via this budget constraint, which represent the remaining measurable variables in the model.
• Finally, there are parameter values within the functions that determine behaviour. When these parameter values shift, they represent a change in behaviour. These changes can be viewed as external shocks to the model, which are not readily forecast.

Wage/Price Ratio Matters

We can simplify matters if we realise that what matters within the model are relative prices. This means that we can look at real wages (nominal wages divided by the goods price index) as well as the real stock of financial assets. 

As an example, the condition for optimality for the household problem in the real business cycle model (equation 6) in the introductory DSGE text by Galí, Jordi* is given in terms of the ratio of wages (W) divided by price (P). This will hold in general, unless the utility function had the unusual structure of depending on nominal values, which is normally avoided. (The exceptions I am aware of might be where money shows up in a utility function.) 

The only place where changes to the price level matter is when financial asset holdings are not indexed to the price level (which is common), and so the real value of financial assets shrinks in the presence of inflation. This lowers the capacity to consume, even if wages rise by the same amount as goods prices.

As an example of the importance of the wage/price ratio, take almost any macro DSGE model (exceptions discussed below) and assume that the initial stock of financial assets is zero. Fix the wage and price series (spot and forecast), and find an optimal solution. If we then scale the wage and price series (e.g., multiply them by 2), we find that the optimal solution has the same real values, but anything in nominal terms (e.g., money holdings) doubles. This works because if we have double the wage rate, the same hours worked gives double the earnings, allowing the purchase of the same number of goods that have also doubled in price. The models that do not have this property have to have nominal values showing up in the utility function, such as nominal money holdings. (This is done to pin down the price level; as this logic demonstrates, these models feature price level indeterminacy unless something is done to pin down the initial price level.)

In real world observations, households do inherit financial assets from the previous time period. However, if we are looking at a monthly time axis -- which we need to do to capture recessions, which are typically short-lived -- the variations in non-equity financial assets in real terms in countries with inflation stability is normally not particularly interesting. We would also need a shift in real wages for the budget constraint to force a drastically different solution.

How Can a Recession Happen?

Most discussions of recessions in DSGE models jumps ahead to discussing the business sector (e.g., productivity), price stickiness, or hand-waving about equilibrium. However, the solution to the model still has to correspond to an optimal solution of the Household Problem.

A recession can be defined as a drop in hours worked versus the previous time period. How can the Household Problem generate such a change? We can pin the cause of the change to being the result to changes to the following (allowing for multiple changes at once).

• By eyeballing the problem, the change in the ratio between wages and goods would have the largest effect. Real wages drop, so potential consumption for the same hours worked is lower. The optimal level is with lower hours worked to reduce the disutility of labour.
• Something can happen to the budget constraint. However, since consumption is smoothed, it is hard to generate a very large effect. The exception might be if we incorporate highly volatile financial assets -- equities. For my discussion herein, I will put that possibility aside, to return to it in my discussion of Roger Farmer's work.
• Finally, behavioural parameters can shift. Even with the same relative prices, households' preferences have shifted towards more leisure.

We can then ask: what does observed economic data look like?

U.S. Relative Price Experience in the 2000's

The figure above shows the employment experience for the two traditional recessions from the 2000s. (I wanted a narrow time frame so that we can easily see the data evolution.) There was a relatively mild recession in 2002, and then the collapse in the Financial Crisis.

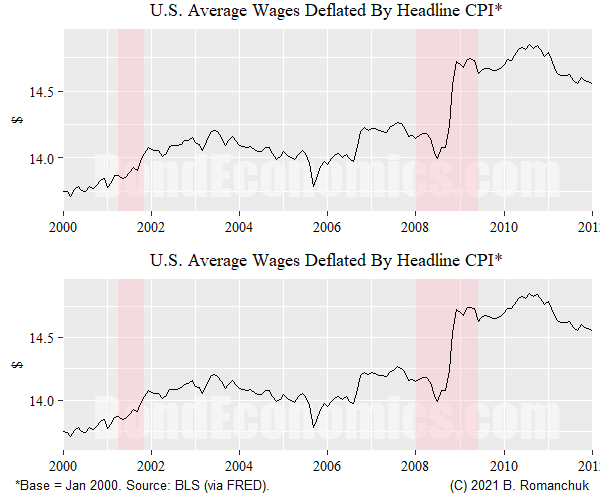
So how well does the price data fit the story outlined above? The figure above examines the behaviour of average wages and core CPI inflation. (Core CPI is excluding food and energy; all items is looked at next.)

The top panel shows familiar percentage changes, the bottom panel shows the ratio. (I normalised the CPI index to 1 in January 2000, so the average wage is shown in "January 2001 dollars.") Looking at this chart, it is safe to say that literally nothing interesting happened in this ratio during the recessionary periods when compared to an expansion.

Since many people are distressed about the concept of core CPI, I repeat the exercise with headline CPI (which includes food and energy). In this case, there is a bit of action -- real wages jumped during the Financial Crisis recession, courtesy of the collapse in gasoline prices.

If we look at the Household Problem, this episode does not fit the story at all: real wages are rising, so workers should be increasing hours worked, not cutting back dramatically.

Admittedly, we are supposed to be working with the entire time histories of wages and prices. However, we do not have any idea what forward wages are doing (we could use breakeven inflation for forward CPI). However, given the nature of the smoothing, it makes no sense to cut back hours now if real wages are close the values in the previous time period.

We are stuck with recessions being explained by two other mechanisms.

1. Dropping equity prices affects the budget constraint. (As per Roger Farmer's body of work.)
2. The parameters in the household sector utility function shifted. Everybody decided that it was a great time to quit work to go on vacation in 2008-2009.

I will discuss Roger Farmer's work elsewhere, leaving us with the "take a vacation" explanation. Even if we put aside the ludicrous nature of the explanation, this leaves us with the recessions being the result of shifts in household preference which cannot be forecast. Recessions just happen. 

We do not need to study Real Analysis to come up with the theory "recessions happen." This is extremely unimpressive, and it is unsurprising that empirical studies of the forecasting capabilities of DSGE models are undewhelming.

Concluding Remarks

The reality is that real wages do not move enough to generate the business cycle movements we have seen in the past decades. Since the core premise of DSGE models is that this the cause of falling employment, we should expect that the models would require radical changes to fit the data.

Technical Appendix: Can We Eliminate this Effect?

One could argue that the models can be tweaked to eliminate the problems I have outlined. Although this is possible, it would likely require junking most of the DSGE macro literature.

One solution is remove the hours worked as a decision variable for households. They optimise consumption given their budget, but take hours worked as given. I would argue that this ends up converging with the stock-flow consistent (SFC) model structure.

Since the previous statement might be surprising, I will briefly explain. The DSGE literature describes models of economic forward pricing. Once we realise that we are not interested in the forward time axis, but rather the historical time axis, it becomes clear that we are only interested in the first period of the DSGE forward pricing solution. Each time period, we solve for a new set of forward prices, but are only interested in the spot price. We can then look at the variables that determine that first period solution. We realise that we can end up with a model that can be approximated by a SFC model.

The problem with households taking hours worked as given blows up the classical understanding of the labour market. Workers can be "forced" to work at any wage by whatever entity sets hours worked. (This unilateral control of the working relationship resembles slavery, and not a model of voluntary labourers.) How can the labour market find "equilibrium"?

One needs to come up with a factor that causes workers to voluntarily cut back hours worked that is not just an unwillingness of a firm to hire them (since that is the domain of the other optimisation problem). I am willing to admit that I am too conventional, but I cannot see any obvious candidates to fill that role within the optimisation problem, other than something like equity market wealth effects.

Footnote:

* Galí, Jordi. Monetary policy, inflation, and the business cycle: an introduction to the new Keynesian framework and its applications. Princeton University Press, 2015.

[Link to first part of article.]

(c) Brian Romanchuk 2021